
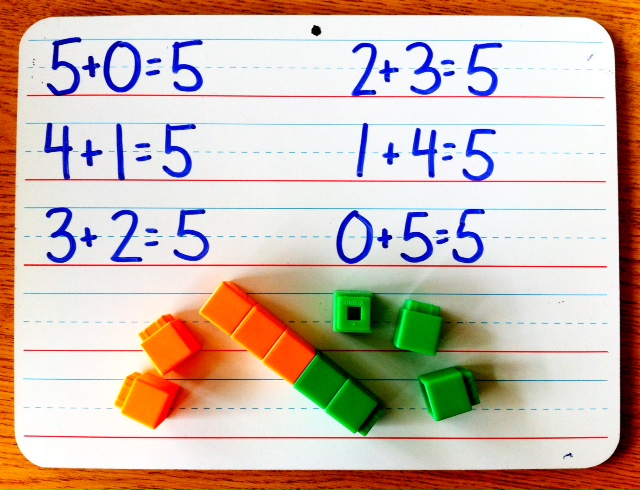
Fourier Analysis has had a significant impact on mathematics and its applications in various fields. For example, it is used to analyze the frequency content of signals and to solve partial differential equations.

The inverse Fourier Transform is given by: f(x) = (1/2π) ∫₋∞⁺∞ F(k) eⁱᵏˣ dk The Fourier Transform has numerous applications in physics, engineering, and applied mathematics. The Fourier Transform of f(x) is given by: F(k) = ∫₋∞⁺∞ f(x) e⁻ⁱᵏˣ dx where k is the frequency variable, and i is the imaginary unit. It allows us to decompose any function f(x) into its constituent frequencies, regardless of whether it is periodic or not.
#COMPOSE DECOMPOSE NUMBERS SERIES#
The Fourier Transform is an extension of the Fourier series to non-periodic functions. This property has numerous applications in signal processing, where signals are often represented as a sum of sinusoidal waves. There is a natural progression here, the more parts that students can break these values into. For example, if we had the number 10, it could be decomposed into any of these two quantities: 1 + 9, 2 + 8, 3 + 7, 4 + 6, or 5 + 5. These coefficients can be calculated using the following formulas: a₀ = (1/π) ∫₀²π f(x) dx aₙ = (1/π) ∫₀²π f(x) cos(nx) dx bₙ = (1/π) ∫₀²π f(x) sin(nx) dx The Fourier series can be used to approximate any periodic function with a finite number of terms. Decomposing numbers is simply taking a value and breaking it into equivalent parts. The Fourier series of a periodic function f(x) with period 2π is given by: f(x) = a₀/2 + Σ(aₙcos(nx) + bₙsin(nx)) where n is a positive integer, and a₀, aₙ, and bₙ are the Fourier coefficients of f(x). The method was developed by French mathematician Joseph Fourier in the early 19th century and has since found numerous applications in various fields of science and engineering. Fourier Analysis is a mathematical technique that decomposes a function into its constituent frequencies.


 0 kommentar(er)
0 kommentar(er)
